

II.1.1 Biographie
II.1.2 Une intuition ?
II.1.3 Présentation et description de l'expérience
II.1.4 Méthode de Römer avec les mesures de 1960
Conclusion

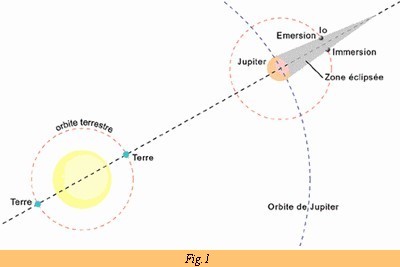



En 1960, lors des mesures, on constate qu’au fur et à mesure que la terre s’éloigne, le cumul de retard de Io (en minute) suivant deux immersions successives est important. Sur le graphique ci-dessous, on remarque bien que le retard maximum est atteint en 16,5 minutes environ entre une opposition c'est-à-dire lorsque Jupiter et la terre sont au plus près et une conjonction (lorsque la terre et Jupiter sont au plus éloignés) suivante.

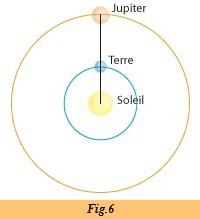
Jupiter en opposition, D = 4,2 UA la dernière éclipse de Io a été observé quelques jours avant. La Terre se trouve en L.
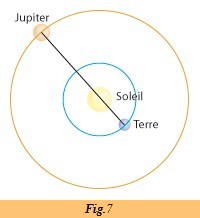
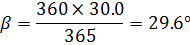
Ainsi,
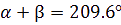
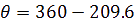
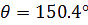
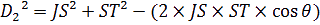
Soit:
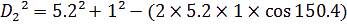
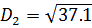
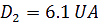
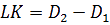
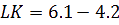
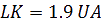
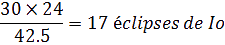

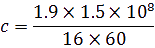
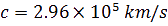
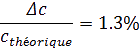
II.1 Römer prouve que la vitesse de la lumière n'est pas infinie
II.1.1 Biographie
II.1.2 Une intuition ?
II.1.3 Présentation et description de l'expérience
II.1.4 Méthode de Römer avec les mesures de 1960
Conclusion

N
é en 1644, Ole (Olaus) Christensen Römer est un astronome
Danois peu connu du grand public, mais qui pourtant a réalisé des exploits
dans le milieu scientifique. Homme pratique, il contribua à ses progrès
tant par la rigueur de ses observations que par la mise au point de nombreux
instruments scientifiques. En 1671, le français Jean Picard, envoyé au Danemark
par l'Académie, proposa au jeune Römer de l'accompagner à Paris. A l’observatoire
de Paris, Römer fut chargé d’étudier le mouvement des satellites de Jupiter
avec Cassini, son Maitre à l’époque.
C'
est alors en 1676 que Römer entreprend une observation d’un
satellite galiléen (en hommage à Galilée), le plus proche de Jupiter, "Io". Il se met
alors à observer les éclipses de Io, c’est-à-dire que le satellite passe dans le cône d’ombre
de Jupiter (figure 1). C'est lorsque Io disparaît (immersion) et réapparaît (émersion)
du cône d'ombre de Jupiter (comme nous le verrons pendant la présentation de l’
expérience). Il remarque alors que la période de révolution de Io à partir de
la durée de son éclipse varie. Il constata que cette période (voisine de 42,5 heures)
variait en fonction de la position de la terre quand on effectuait la mesure. Ce
résultat était bien sûr en contradiction avec les lois de Kepler et les tables de
Cassini (date "exacte" des éclipses de Io) qui stipulaient que la période de
révolution du satellite était constante. C’est alors que Römer eu une intuition
géniale : Il faudrait tenir compte du parcours de la lumière !


A
insi, Römer avec sa lunette astronomique observe les immersions
et les émersions de Io à divers instants. Lorsque Io disparait dans le cône d’ombre
c’est l’immersion et dès qu’elle réapparait c’est l’émersion.
C
omme Römer remarque que la durée de révolution de Io augmente
lorsque la terre s’éloigne de Jupiter, cela voudrait signifier que la lumière ait
mis plus de temps à parvenir jusqu’à la terre. Ainsi, dans son rapport publié dans
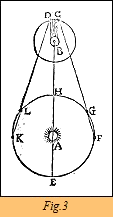
"le journal des savants" (figure 4), Römer explique que si A le Soleil, B Jupiter et C le
premier satellite qui rentre dans l'ombre de Jupiter, pour en sortir en D et EFGHKL,
la Terre placée à différentes distances de Jupiter, supposé que la Terre étant en L
lors de la première quadrature LK et observant la première émersion (sortie de l’ombre)
de Io en D et 42,5 heures plus tard la terre se trouvant en K, alors fondant son
hypothèse sur la révolution de Io plus longue, il est "manifeste que la lumière prend
un certain temps pour traverser l'intervalle LK". Römer admet que la lumière effectue
le parcours LK sur un temps t’ le temps de retard. Ainsi, il annonce en 1676 à l'Académie
royale des sciences que l'éclipse du premier satellite de Jupiter, prévue
pour le 9 novembre suivant, se produira avec 10 minutes de retard ce qui fut chose faite…



N
ous allons ici appliquer la méthode de Römer. Nous allons nous appuyer sur les
données de l’expérience de 1960 nous donnant des données exactes car Römer avait en
effet effectué tellement de mesures que nous ne possédons pas de chiffres exactes.
En 1960, lors des mesures, on constate qu’au fur et à mesure que la terre s’éloigne, le cumul de retard de Io (en minute) suivant deux immersions successives est important. Sur le graphique ci-dessous, on remarque bien que le retard maximum est atteint en 16,5 minutes environ entre une opposition c'est-à-dire lorsque Jupiter et la terre sont au plus près et une conjonction (lorsque la terre et Jupiter sont au plus éloignés) suivante.

O
bservons sur le graphique ci-dessus : on remarque qu’à partir de 50
éclipses de Io observées, le retard de l’apparition de celles-ci est nul. On peut donc
dire que la terre se trouve au plus près de Jupiter. Or lorsque la terre est au plus
loin de Jupiter, c'est-à-dire en conjonction (figure 5) le retard maximal t’ atteint l’ordre
de 16,5 minutes vers 160 éclipses. Ainsi, la lumière provenant de Io aurait mis 16,5
minutes de plus pour parvenir jusqu’à la terre. Or, mettons nous à la place de Römer,
quand la terre est en conjonction avec le soleil, les éclipses de Io sont inobservables.
Observer Jupiter dans ces conditions équivaudrait à se bruler la rétine de l'œil avec
la lumière du soleil concentrée par le télescope. Il faut attendre un peu après la
conjonction pour voir réapparaitre Jupiter et réobserver Io.
A
l’opposition, Jupiter la terre et le soleil sont alignés donc
l’observation de Io est possible alors on trouve une révolution de Io dans les environs
de 42,5 heures puisque t’ = 0. Dans le but de représenter les études décrites dans le
rapport de Römer nous nommerons les positions de la terre L et K.
D
onc les distances entre les astres sont telles que :
Distance Terre soleil : TS = 1 UA*
Distance Jupiter soleil : JS = 5,2 UA
Distance terre Jupiter : TJ = 5,2-1 = 4.2 UA
On notera TJ = D1
*rappel : une Unité Astronomique (UA) équivaut à
150 millions de kilomètres (distance terre-soleil)
Distance Jupiter soleil : JS = 5,2 UA
Distance terre Jupiter : TJ = 5,2-1 = 4.2 UA
On notera TJ = D1
*rappel : une Unité Astronomique (UA) équivaut à
150 millions de kilomètres (distance terre-soleil)

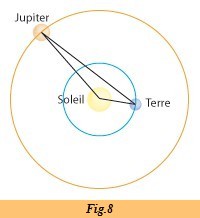
Jupiter en opposition, D = 4,2 UA la dernière éclipse de Io a été observé quelques jours avant. La Terre se trouve en L.
C
omme Jupiter aussi avance doucement sur son orbite,
la conjonction s’effectuera à un peu plus de la moitié d’une année sidérale
(365 jours). Une fois la terre arrivée en conjonction avec la planète Jupiter,
on peut alors dire qu’elle a voyagé pendant 195 jours. Car en effet, si
l’on débute à 50 éclipses de Io à l’opposition pour finir à 160 environ
à la conjonction, il y a :
160-50 = 110
éclipses de Io entre opposition et conjonction
Soit :
110 x 42,5/24 = 195
jours se sont écoulés.

A
insi, lors de la conjonction Jupiter, le Soleil et la Terre forment
un angle a = 180°. On a alors au niveau des distances :
JS = 5,2 UA
ST = 1 UA
JT = 6,2 UA
ST = 1 UA
JT = 6,2 UA
O
r ici, Jupiter est inobservable. Il faut donc attendre un peu après
la conjonction pour pouvoir réobserver Io correctement. Nous allons prendre 30 jours
d’attente soit environ un mois afin que la terre soit suffisamment avancée. Ainsi, la
Terre arrive en K. Pour faciliter le calcul, nous calculons le nouvel angle ß balayé par la terre en 30,0 jours.
Pour une orbite de 360° qui équivaut à 365 jours, alors :
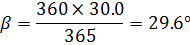
Ainsi,
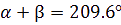
D
onc dans le triangle JST, l’angle JST qu’on nommera &theta vaut :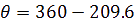
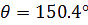
N
ous cherchons maintenant la distance Jupiter-Terre qu’on nommera D2. Connaissant
JS et ST, D’après le théorème d’al-Kashi (que l'on démontre dans l’intermède mathématique), dans le triangle JST on a :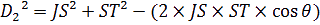
Soit:
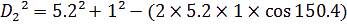
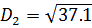
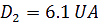
A
insi, on trouve une distance entre Jupiter et la terre de 6,1 UA 30 jours après la
conjonction. Pour en revenir à l’affirmation de Römer dans son rapport, nous cherchons LK :
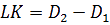
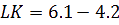
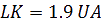
A
yant LK il nous manque plus que le retard de l’éclipse de Io noté t’ pour trouver
un ordre de grandeur de la vitesse de la lumière.
On calcul, donc 30 jours équivaut à :
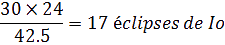
D
onc sur notre graphique, la 17ème éclipse de Io après la conjonction se situe à l’éclipse n°177
et avec un retard d’apparition t’= 16 minutes. Ainsi, on applique la formule donnée par Römer dans son rapport :

Donc :
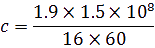
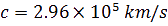
N
ous trouvons alors grâce à la méthode de Römer, une valeur très proche de la vitesse de la
lumière théorique d’aujourd’hui. Ici, nous avons un pourcentage d’erreur de :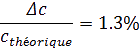
N
otre résultat obtenu est bon car il est proche de la valeur théorique. Evidemment, il ne faut pas
oublier que nous avons utilisé les mesures de 1960 donc des mesures assez récentes et précises, car à l’époque Römer trouva sur
l’ensemble de ses mesures (environ 40), un ordre de grandeur de la vitesse de la lumière d’environ 230000 km /s
soit une erreur relative de 22 % ce qui était pas mal du tout pour l’époque. Ainsi, la précision de notre
résultat montre bien la pertinence d’une telle expérience astronomique et le génie de son auteur.
E
n revanche, Römer se refusa à écrire dans son rapport tout calcul de la vitesse de la lumière.
Il se contenta seulement de prouver que la lumière a bien une vitesse finie. Ce qui était déjà une très grande prouesse.
Car depuis l’antiquité, on admettait que la lumière avait une vitesse infinie. Jean-Dominique Cassini, le maitre de Römer,
continua d'affirmer longtemps que les irrégularités des éclipses de Io sont dues à des anomalies dans la force
d'attraction gravitationnelle de Jupiter sur Io. Il fallut attendre les travaux de James Bradley en 1729, et de
Jean-Baptiste Delambre en 1809 pour que la thèse de Römer l'emporte enfin... Seul Galilée avait eu cette intuition
mais par faute de moyens techniques il n'a rien prouvé. Ainsi, l'idée d'une vitesse finie pour la lumière était
définitivement acquise.