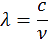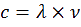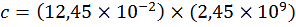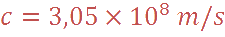
(on en conclut que la position de la lamelle de fromage n'a aucun effet sur l'expérience)
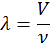
(où λ est est en m, v en Hz et V en m/s)
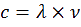
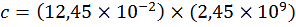
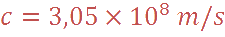
IV.3 Notre expérience et notre mesure de la vitesse de la lumière
A
près avoir défini les ondes stationnaires, nous montrerons dans cette dernière partie comment
le FMO, nous permet aujourd’hui de calculer facilement la vitesse de la lumière.
A
u cœur d’un FMO, on peut observer qu’en utilisant le plateau tournant la nourriture est chauffée
de manière uniforme. Si on retire le plateau et tous les moyens de dispersion des micro-ondes,
la nourriture ne va pas être chauffée uniformément. Justement, sur n’importe qu’elle aliment (à
condition qu’il soit composé d’eau !), il va y avoir présence de zone plus chaudes qu’on nommera
points chauds. Si on observe ces points chauds, on peut même remarquer qu’à priori ils seraient
séparés d’une distance régulière.

N
ous savons que les micro-ondes deviennent des ondes stationnaires dans le FMO, celles-ci même qui
chauffent les aliments. Justement, les ayant déjà étudiées nous avons remarqué que les distances
entre chaque ventre et chaque nœud d’une onde stationnaire sont régulières.
D
’après ces deux faits, nous pouvons alors nous demander si la distance entre chaque point chaud formé
est en relation avec la distance entre chaque ventre ou nœud de ces ondes stationnaires.
A
près plus amples recherches, nous avons appris que l’on trouve des points chauds aux ventres de
l’onde stationnaire. N’ayant pas les moyens de prouver ce fait nous sommes obligés ici de l’admettre.
Cela signifie que les molécules d’eau s’agitent très fortement aux ventres de l’onde stationnaire.
Les points chauds, ainsi formés par l’agitation de ces molécules au maximum du champ électrique,
nous permettent de montrer le passage des différentes ondes stationnaires. On devrait alors trouver
sur les aliments (à condition qu’il n’y ait aucun moyen de dispersion), des lignes sur lesquelles
des points chauds se seraient formés, espacés de manière régulière.
L
’expérience est réalisée dans le but de mesurer la distance entre chaque point chaud, soit la distance
entre chaque ventre de l’onde stationnaire, étant connu : λ/2.
C
ette expérience peut être réalisée à l’aide de tous les aliments (à condition qu’ils contiennent des
molécules d’eau). Nous utiliserons ici du chocolat mais aussi et surtout du fromage.
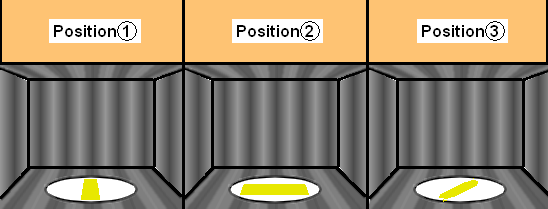
P
our réaliser l’expérience on dispose une lamelle de fromage d’à peu près un centimètre d’épaisseur,
de 16,5 centimètres de long et de deux ou trois centimètres de largeur sur un support plat que l’on place
dans le FMO. Après quelques secondes (à peu près quinze secondes), à 1 000 watt, sans le plateau tournant
ou en l’ayant désactivé, on récupère la lamelle de fromage. On remarque alors trois points chauds alignés,
preuve de la présence de l’onde stationnaire.
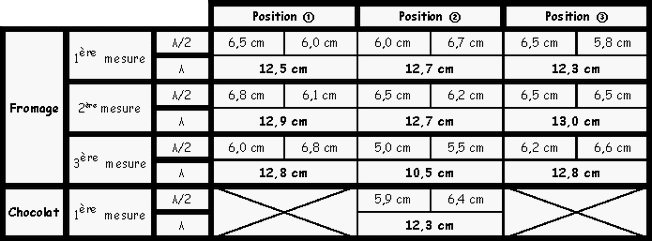
S
uite à cette expérience, on remarque sur le fromage trois points chauds, alignés et écartés de distances
assez régulières. Pour plus de clarté nous avons réalisé le tableau ci-dessous. Il nous permet de noter
tous nos résultats et réaliser une moyenne des distances entres les points chauds. Ainsi notre mesure de
λ/2 ou λ est plus précise.
P
our prouver que les ondes stationnaires sont présentes dans tous le FMO, nous avons réalisé différentes
mesures en plaçant le fromage dans différentes positions.


L
a mesure avec le chocolat peut être réalisée. L’avantage avec le chocolat, c’est que l’on peut voir plus
nettement la différence entre zones chaudes et froides. Cela est dû au fait que le chocolat est composé
de beaucoup moins d’eau que d’autres aliments, la conduction étant ainsi plus lente. Ainsi un chocolat
au lait fondra plus vite qu’un chocolat noir.
E
n réalisant notre expérience sur une tablette de chocolat noir, nous retrouvons des mesures très proches
du chocolat. Nos différentes mesures nous donnent pour :
λ
/2 : 5,9 cm, 6,4 cm
O
n a ainsi pour λ: 12,3 cm
C
es mesures sont donc tout à fait cohérentes par rapport à celles effectuées sur le fromage.
N
ous pouvons alors établir une moyenne de toutes ces valeurs pour une plus grande précision.
O
n trouve ainsi pour λ, 12,45 cm. Elle est la valeur finale de notre expérience.
L
’expérience nous a permis de dégager une mesure, celle de λ : la longeur d'onde. C’est en effet,
la connaissance de cette mesure qui va nous permettre
de calculer approximativement la vitesse de la lumière. La vitesse est seulement approximative
car nos mesures expérimentales ne peuvent être parfaites.
L
a vitesse de la lumière peut être calculée en connaissance de deux termes : λ, et la fréquence
v (nu) à laquelle les aliments sont soumis.
C
es termes sont regroupés en un même calcul :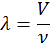
O
n sait que la fréquence des micros ondes est 2,45 GHz. On peut alors calculer la célérité de
la lumière :