

II.3.1 Biographie
II.3.2 Présentation de l'expérience
II.3.3 Description de l'expérience
II.3.4 Calculs
Conclusion







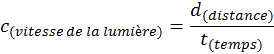
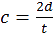
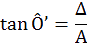
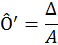
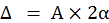
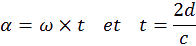
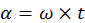
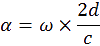
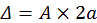
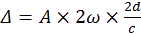
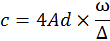
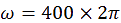
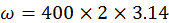
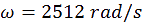
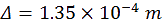
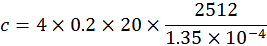
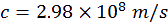
c = 299 792 458 m/s.
II.3 Foucault précise la vitesse de la lumière
II.3.1 Biographie
II.3.2 Présentation de l'expérience
II.3.3 Description de l'expérience
II.3.4 Calculs
Conclusion

Fig.1, Léon Foucault
N
é le 18 septembre 1819 Jean Bernard Léon Foucault (figure1) est un autodidacte physicien et astronome
Français. Ayant commencé des études de médecine jeune, il les abandonne pour se lancer dans
la science physique. Notamment, il étudie l’optique avec sa fameuse photographie Daguerre ou
encore l’étude infrarouge du soleil avec son grand ami Fizeau . Foucault est surtout reconnu
pour sa célèbre expérience du pendule où il démontre la rotation de la terre en 1851 (figure 2).
Par ailleurs, en 1855 nous devons à Foucault l’invention du télescope moderne qui devient
largement plus performant que ses précédants (figure 3).
C
’est en 1850 que Foucault entreprend
une très ingénieuse expérience consistant à étudier un rayon de lumière réfléchi grâce à un
puissant miroir tournant. Il prouve ainsi que la lumière se déplace moins vite dans l’eau
que dans l’air. Nous allons ainsi voir que Foucault prouve enfin la théorie ondulatoire
de la lumière. Mais encore, en 1862 Foucault réalise en améliorant le système de son miroir
tournant la première mesure très précise de la vitesse de la lumière. En 1964 il est admis
à l’académie des sciences et décède quatre ans plus tard. L’intuition extraordinaire de Foucault
et de ses incroyables expériences font de lui l'un des plus grand savants du 19ème siècle.

Fig.2

Fig.3
E
n 1850 Foucault réalise sa première expérience. Elle rend possible la comparaison entre
la vitesse de la lumière dans l’eau et dans l’air comme vue dans la partie I. Cette première
expérience ne lui a permis de réaliser qu’une estimation qualitative de la célérité de
la lumière.
A
près celle-ci, Foucault est conscient du potentiel de son expérience. C’est ainsi qu’en
septembre 1862, après d’importantes innovations techniques notamment de son fameux miroir
tournant, il réalise à nouveau son expérience. A l'observatoire de Paris, accompagné de
l'ingénieur Froment (réalisateur de certains objets du dispositif) et le facteur d'orgues
Cavaillé-Coll (inventeur d’un système de soufflerie très stable, permettant l’alimentation
de la turbine à air comprimé entraînant le miroir tournant), son expérience réussit.
I
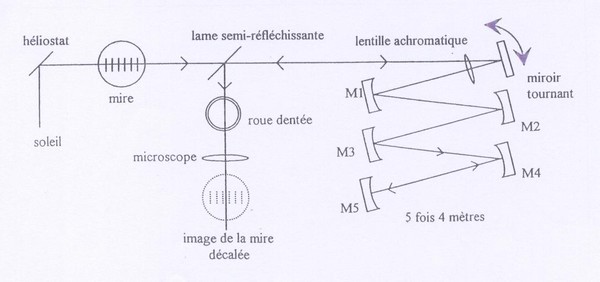
l utilise pour ce faire un dispositif en partie diffèrent mais gardant le même principe.
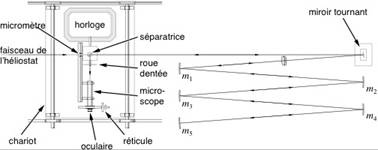
Le dispositif est en effet composé de cinq miroirs concaves (figure 7) permettant
d’augmenter le trajet du faisceau de lumière. L’expérience gagne ainsi en précision. Il y a
aussi présence d’un miroir tournant à grande vitesse (24 000 tours/minute). L’expérience a été réalisé avec
une lentille et l’élément qui a été le plus amélioré, l’horloge (figure 5), composée
d’un micromètre, un microscope, une roue dentée et une lame semi réfléchissante (pour les
éléments principaux). Cette expérience est assez intéressante car son dispositif ne prend
pas énormément de place. C’est pour cela et aussi pour sa précision qu’à
cette époque cette expérience dépasse celle de Fizeau basée sur une roue dentée.

Fig.4, miroirs fixes

Fig.5, horloge

Fig.6, miroir tournant

Fig.7
A
ujourd’hui une représentation de cette expérience est exposée au musée des arts et métiers.
(l’originale est à l’Observatoire de Paris). (figure 7)

Fig.8, schématisation du dispositif de 1862 (avec détails de l’horloge)
C
ette expérience doit beaucoup aux constructeurs du miroir tournant, utilisé, mais bien sûr
aussi à l’ingéniosité de Foucault dans sa manière de l’utiliser. Ce miroir tournant inventé
par l’anglais Charles Wheatstone permet d’observer des phénomènes très rapides. C’est dans
ce but qu’il est beaucoup utilisé au XIXème siècle par d’autres scientifiques cherchant la vitesse de la lumière.
L
e principe de l'expérience est simple :
la lumière du soleil ou d’une quelconque source lumineuse est capté par l’héliostat (voir
schéma). Une fois dans l’horloge le rayon passe à travers une mire graduée et est dévié
ensuite vers le microscope ou vers le miroir tournant, en fonction de la vitesse de rotation
du miroir tournant. Dans le premier cas, le miroir tournant est à l’arrêt. La lumière revient
donc sur une lame semi réfléchissante puis dans l’oculaire de l’observateur. Le rayon à alors
pris le même chemin qu’à son aller. Dans le second cas, le miroir tournant est mis en rotation.
La lumière se réfléchit sur le miroir tournant, puis sur chacun des cinq miroirs concaves. Il
revient alors en sens inverse après le dernier miroir. A ce moment là le miroir tournant a
tourné d’un certain nombre de degrés par rapport à sa position initiale. Le faisceau revient
vers la lame semi-réfléchissante, mais avec un décalage (le rayon ne prend pas le même chemin
qu’à l’aller).
O
n admettra, selon les lois de Descartes, que quand le rayon lumineux se réfléchit sur le miroir
tournant, les angles i (d’incidence) et r (de réflexion) sont dans le même plan et sont égaux,
d’après le principe de réflexion (partie I).

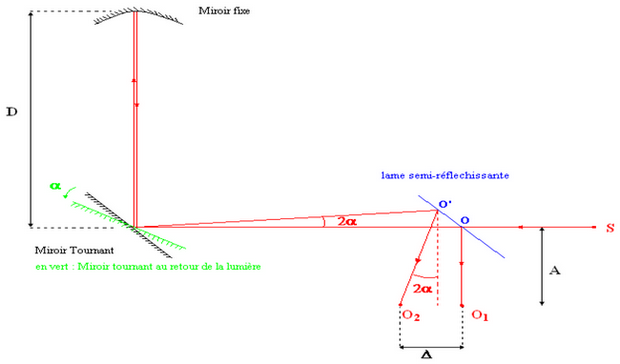
Fig.9, schématisation précise de l’expérience de Foucault
(avec détail du système d’horlogerie).
(avec détail du système d’horlogerie).
P
our l’observateur, plusieurs visions sont alors possibles. Lorsque le miroir tournant a une
vitesse de rotation faible ou nulle, le rayon lumineux est visible mais seulement par alternance
lorsque le miroir tournant est en face des miroirs fixes, soit sa position initiale.
Si la vitesse de rotation du miroir augmente suffisamment, le temps que met le faisceau lumineux
pour faire un aller et retour entre les miroirs fixes et le miroir tournant n’est plus négligeable.
C’est ainsi, que le miroir tournant aura légèrement tourné, quand le rayon lumineux reviendra sur
lui. L’observateur pourra alors remarquer un décalage du faisceau lumineux, dans l’oculaire. On
peut alors affirmer que la lumière a une vitesse et c’est à partir de cette différence que Foucault
va la calculer.
L
e calcul de la vitesse de la lumière n’est possible qu’en connaissance de la vitesse de rotation
du miroir tournant. Pour ce faire, Foucault utilise le mouvement de l’horloge. En effet, elle permet
de mettre en rotation une roue dentée à une vitesse de 400 tours par secondes (vitesse de rotation
que doit atteindre le miroir tournant pour qu’un décalage soit observable).
C
ette roue se superpose avec l’image provenant du miroir tournant. Lorsque la vitesse de rotation
du miroir atteint la vitesse de 400 tours par seconde, soit la vitesse égale à celle de la roue
dentée, un effet stroboscopique rend la roue dentée immobile, une dent se substituant exactement
à la précédente. Ce moyen permet au miroir d’être réglé avec précision.
I
l ne reste alors plus qu’à mesurer la déviation du rayon lumineux. Elle est possible grâce au
décalage de la mire graduée par rapport à sa position initiale. Ce décalage est observé précisément
par une croisée de fils placée dans l’oculaire. Cette observation est visible si l'on compare les
mires en fonction de la vitesse de rotation du miroir tournant. Lorsque le miroir est immobile, la
mire est réglée de façon à ce que la croisée des fils pointe précisément la graduation centrale.
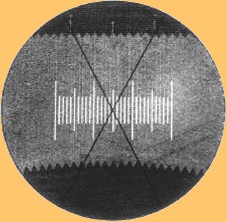
Lorsque le miroir tournant est mis en rotation, on peut mesurer le déplacement de la mire avec une bonne précision. (figure 10)

Fig.10
I
mage d’une mire graduée par rapport à une croisée de fils placée dans l’oculaire, quand le miroir
tournant est en rotation (vitesse de rotation= 400 tours par secondes)[Fig10]. Ici le décalage n’est pas
flagrant mais il est visible, puisqu’il est de 1,35.10-4m.

Fig.11, schéma de l’expérience de Foucault
C
onnaissant ainsi le déplacement du rayon lumineux, la vitesse du miroir tournant et la longueur
du parcours de la lumière, Foucault a pu calculer la vitesse de la lumière.

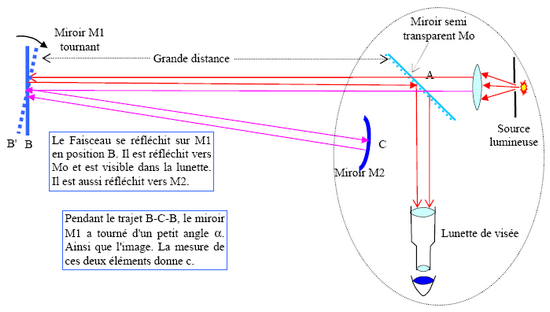
Fig.12, schéma de l’expérience de Foucault (avec détails pour calcul de c)
G
râce à cette représentation graphique, on peut remarquer que S, correspond à la source lumineuse. O1,
est l’image de la source observée dans l’oculaire du microscope, lorsque le miroir tournant est immobile.
O2, est aussi cette image mais observée lorsque le miroir tournant a une vitesse de rotation ω. Δ est
la distance entre O1 et O2, c’est-à-dire le décalage du faisceau lumineux. Enfin, A est la distance entre
la lame semi-réfléchissante et l’oculaire. On note alors ω, la vitesse de rotation du miroir tournant, et
t le temps mis au faisceau lumineux pour parcourir une distance 2d à la vitesse c.
C
et ensemble nous permet de faire ressortir une égalité, pour le calcul de la vitesse de la lumière :
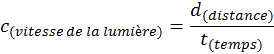
O
n a donc ici :
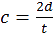
D
e plus, on sait que α est l’angle de la rotation effectué par le miroir tournant durant un temps t.
S
upposant que l’angle α est petit (il tend vers 0), on peut confondre les points O et O’. On a donc: O = O’
. Par trigonométrie dans le triangle rectangle (O’ O2 O1) on a alors :
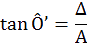
M
ais on sait d’après une relation mathématique (que l'on démontre dans
l’intermède mathématique) que tan (Ô’) = Ô’ (Ô’ étant toujours considéré comme un angle).
S
i on se place maintenant dans le triangle, O’O2 O1, on connaît l’angle O’. De plus on
sait que [O2 O1] mesure une distance Δ et que [OO1] mesure une distance A.
E
tant donné que l’on se trouve dans un triangle rectangle en O1, on a l’égalité suivante :
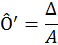
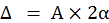
O
n sait alors que :
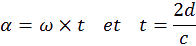
Donc :
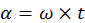
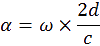
S
i on remplace α, dans l’égalité Δ = A × 2α, on trouve alors la vitesse de la lumière c.
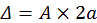
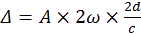
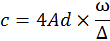
I
l ne reste alors plus qu’à remplacer par les valeurs numériques connues. La vitesse de
rotation du miroir tournant étant de 400 tours par secondes, convertie en radians elle est de :
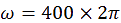
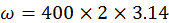
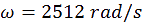
L
a distance d totale entre les cinq miroirs est de 20 mètres car les miroirs sont espacés les uns
des autres par 4 mètres. La distance A, entre l’oculaire de l’observateur et la lame semi-
réfléchissante est mesurée à 20centimètres soit 0,2 mètres. Enfin, la mire graduée indique
un décalage de :
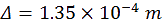
S
i on remplace on obtient :
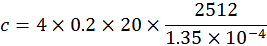
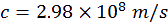
L
a mesure de la vitesse de la lumière, annoncé par Foucault marque une erreur de 0.6 %.
D
ouze années après sa première expérience, déjà concluante. Foucault, autodidacte, comme
son ami Fizeau réussit une mesure encore plus précise de la mesure de la vitesse de la lumière.
Il obtient une précision encore jamais vue, une erreur de seulement 0,6 % par rapport à
la valeur théorique. A cette époque, Foucault, grâce
à son miroir tournant marque un nouveau pas dans la physique et la précision. C’est dans ce
sens que ses successeurs, ne cesserons de préciser la vitesse de la lumière jusqu’à celle admise
aujourd’hui :c = 299 792 458 m/s.