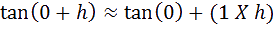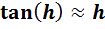
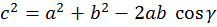
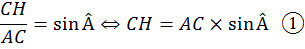
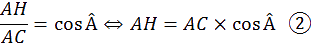
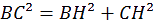

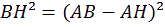
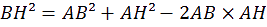
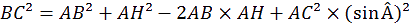
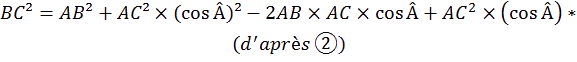
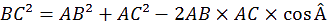
cos (Â)² + sin (Â)² = 1
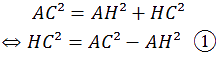
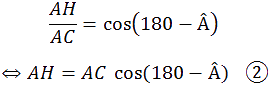
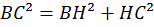
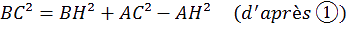
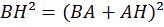
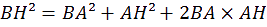
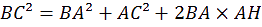
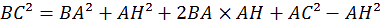
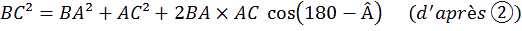
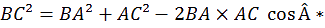
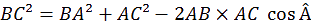
En effet:
Le calcul infinitésimal de Leibniz
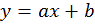
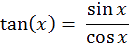
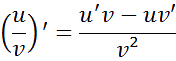
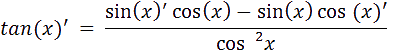
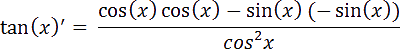
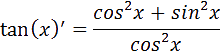
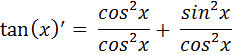
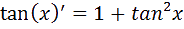
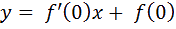
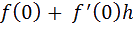
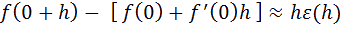
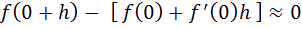
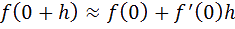
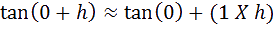
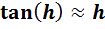
Intermède mathématique
D
émontré par la mathématicien perse Ghiyath Al-Kashi, le théorème d’al-Kashi
ou loi des cosinus est une généralisation du théorème de Pythagore dans les
triangle non rectangles.

S
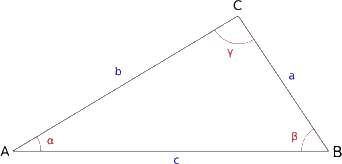
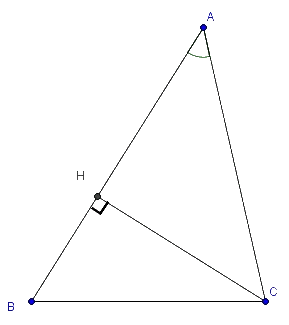
oit un triangle ABC, dans lequel on utilise les notations usuelles exposées
sur la figure 1 : d'une part α, β et γ pour les angles et, d'autre part, a,
b et c pour les côtés respectivement opposés à ces angles. Alors, le théorème
d'al-Kashi s'énonce de la façon suivante :
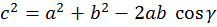
I
l existe deux cas possibles : un triangle formé de trois angles aigus et un
triangle formé d'un angle obtu et deux aigus.
Démonstration avec un triangle ayant trois angles aigus

D
ans le triangle rectangle AHC on a :
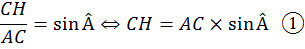
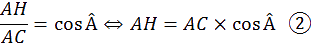
D
onc dans le triangle BHC, on a :
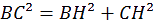

M
ais :
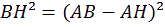
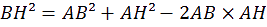
D'où :
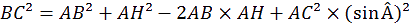
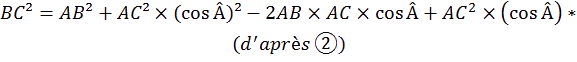
O
n retrouve bien la relation d’Al-Kashi :
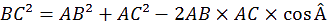
* O
n a utilisé la loi fondamentale de la trigonométrie : cos²Â + sin²Â = 1 ou
encore
D
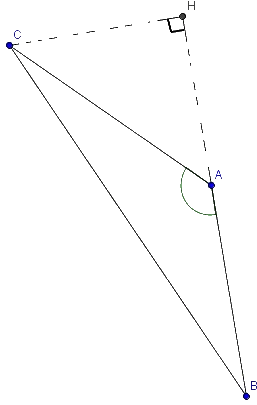
émonstration avec un triangle ayant un angle obtu et deux angles aigus

D
ans le triangle rectangle AHC on a :
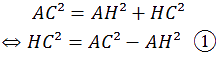
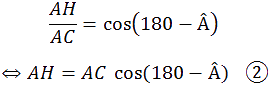
D
onc dans le triangle BAC on a :
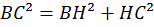
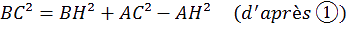
M
ais :
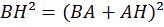
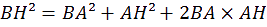
D'où :
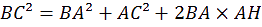
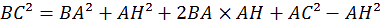
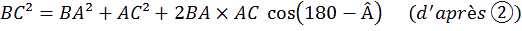
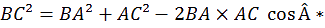
O
n retrouve bien la relation d’Al-Kashi :
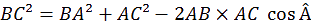
* I
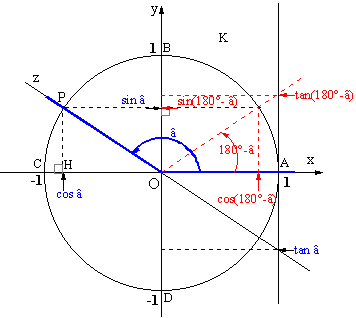
ci, on a utilisé une propriété de trigonométrie que l’on retrouve dans le cercle trigonométrique :En effet:

O
n remarque bien que cos(â) est symétrique à cos(180 – â) par rapport à l'axe des ordonnées, donc ils sont opposés.
C
e qui veut dire que cos(180 – Â) = -cos(Â), d’où le résultat admit dans la démonstration.

P
ar rapport à l’expérience de Foucault on admet un angle très petit au voisinage de 0, ce qui implique que l’on représente
cet angle en un point d’abscisse au voisinage aussi de 0. Cela explique donc que l’on se place dans un système proche de 0.

D
ans un repère orthonormé d’origine O, on peut tracer la fonction tangente d’équation y = tan(h)
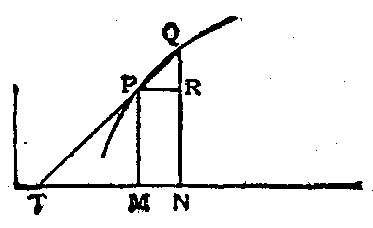
U
n point Mh de cette courbe d’abscisse h peut alors être placé. Son ordonnée est f(0+h) ou tan(0+h) comme nous sommes sur
la courbe de la fonction tangente. Nous pouvons alors tracer la tangente T à la courbe tangente, d’équation:
N
ous situant sur la tangente de la fonction tangente par définition le coefficient directeur de cette droite est la dérivée
de tan(x).
Soit :
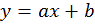
O
n sait que :
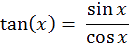
D
onc pour trouver la dérivée de tan(x) on fait agir la formule suivante vue en cours :
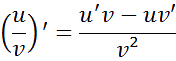
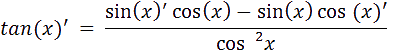
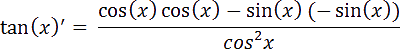
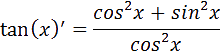
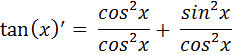
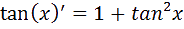
L
’équation de la tangente à la courbe tangente est donc :
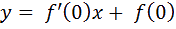
(y = x pour la fonction tangente).
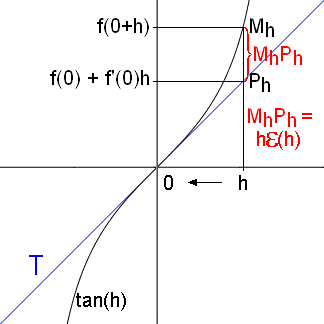
S
i on prend alors un point Ph, sur la tangente T, d’abscisse h son ordonnée est :
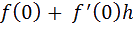
S
oit la fonction tangente et sa tangente, si on fait tendre h vers 0, la différence (hε(h)) tend aussi vers 0.
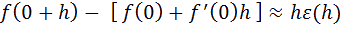
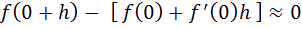
A
lors :
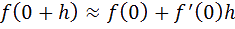
D
onc