

IV.2.1 Représentation mécanique : la corde
IV.2.2 Les ondes stationnaires : la théorie
IV.2.3 Les ondes stationnaires dans le four à micro-ondes
IV.2 Les ondes stationnaires au cœur du four à micro-ondes
IV.2.1 Représentation mécanique : la corde
IV.2.2 Les ondes stationnaires : la théorie
IV.2.3 Les ondes stationnaires dans le four à micro-ondes
N
ous chercherons dans cette partie à trouver la représentation des micro-ondes émises par le four
à micro-ondes (FMO). Rappelons que la micro onde est une onde électromagnétique correspondant à
la superposition du champ magnétique et du champ électrique. Nous avons déjà parlé de l’onde
électromagnétique dans le FMO, mais maintenant, nous allons voir comment celle-ci se meut au
coeur du FMO. Nous poserons ainsi les bases de notre expérience.
S
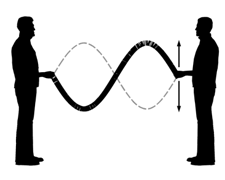
ur Terre, nous pouvons représenter assez aisément une onde. En effet, si deux personnes se tendent
une corde et qu’ils exercent sur elle un mouvement de bas en haut, la corde va réaliser un mouvement
spécial. Si on se place en face des deux personnes, en tant qu’observateur, on remarque que la
corde réalise des vagues régulières : c’est le mouvement d’une onde (figure 1).

Fig.1
E
n nous appuyant sur la situation vue ci-dessus, et en admettant maintenant que l’onde
incidente est une onde progressive sinusoïdale de fréquence f, sa célérité est v et
sa longueur d’onde λ=v/f.
Q
uand une onde incidente va rencontrer une paroi, elle va être réfléchie en sens
contraire. L’onde ainsi produite est une onde réfléchie. Ces deux ondes incidentes
et réfléchies vont ainsi se superposer et générer une onde stationnaire.

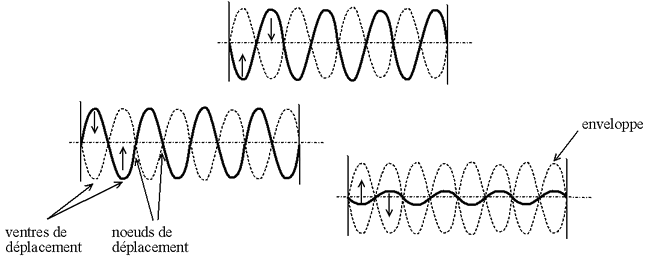
Fig.2
D
e plus, l’enveloppe de l’onde stationnaire est particulière puisqu’elle est constituée de fuseaux. (figure 2)
Un fuseau étant centré sur un ventre et des nœuds voisins formant ses extrémités. Les distances
séparant chaque ventre et nœud peuvent être connues. Nous les admettrons car étant dans l’impossibilité
de les démontrer. Les ventres sont situés aux distances λ /4, 3λ/4, 5λ/4 d’une extrémité fixe de la
corde. Les nœuds quant à eux sont situés aux distances 0, λ/2, 2λ/2, 3λ/2 d’une extrémité fixe de la
corde. La distance entre deux nœuds voisins ou deux ventres voisins est égale à λ/2 : c’est la longueur
d’un fuseau (longueur entre deux noeuds ou deux ventres). La régularité de ces distances est à la base
de nos résultats.
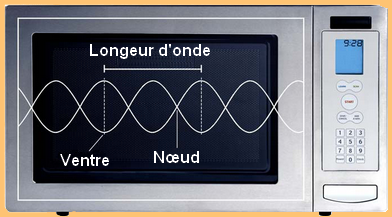
G
râce aux explications apportées par les deux premières parties, on peut comprendre plus aisément la
formation d’ondes stationnaires dans le FMO. En effet, en se plaçant dans le FMO, les ondes stationnaires
vont se former grâce à ses parois qui vont réfléchir les micro-ondes et ainsi générer ces ondes stationnaires.

Fig.3