

Introduction
I.2.1 Les ondes lumineuses selon Huygens
I.2.2 Réflexion, réfraction : le principe de Huygens
I.2.2.1 La réflexion selon Huygens
I.2.2.2 La réfraction selon Huygens
Conclusion



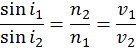
I.2
Les idées de la théorie ondulatoire
Introduction
I.2.1 Les ondes lumineuses selon Huygens
I.2.2 Réflexion, réfraction : le principe de Huygens
I.2.2.1 La réflexion selon Huygens
I.2.2.2 La réfraction selon Huygens
Conclusion
D
éveloppée par le hollandais Christiaan Huygens (figure 1) en 1678, la théorie ondulatoire est une véritable
révolution dans les idées en physique. Pour Huygens, la lumière apparait comme une vibration se
transmettant de proche en proche dans un milieu : l’éther (milieu fluide contenu dans tout l’univers).
L’éther serait un ensemble de particules qui oscilleraient donnant la lumière.
Fig.1, Christiaan Huygens
D'
une manière générale, une onde est une perturbation qui se propage et transporte de l’énergie.
Pour l’instant, l’onde est encore un concept mal connu. Malgré l’aveuglement de la théorie corpusculaire,
cette nouvelle théorie publiée en 1690 dans le "traité de la lumière" permet contrairement à l’autre,
un siècle plus tard, de rendre compte des phénomènes de diffraction, d’interférences et induit
forcément une vitesse finie de propagation. Aussi, cette théorie permet de nouveau une interprétation
de la réflexion mais surtout une nouvelle interprétation de la réfraction cette fois en affirmant que
la vitesse de propagation de la lumière doit diminuer selon la densité du milieu traversé.
P
our Huygens, les ondes lumineuses sont mécaniquement analogues aux ondes mécaniques progressives
longitudinales comme la propagation du son dans l’air (figure 3). D’une manière générale, on appelle onde mécanique
progressive, le phénomène de propagation d'une perturbation dans un milieu matériel sans transport de
matière. Il existe deux types de ces ondes :
•
Les ondes transversales : Celles-ci sont transversales, lorsque les points du milieu se déplacent
perpendiculairement à la direction de propagation comme lorsque qu’un caillou tombe dans l’eau. (figure 2)
Fig.2
•
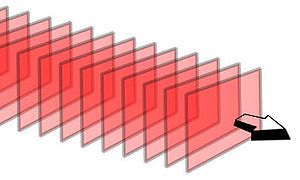
Les ondes longitudinales : Une onde est longitudinale lorsque les points du milieu se déplacent
parallèlement à la direction de propagation. Comme la propagation du son dans l’air. (figure 3)
Fig.3
U
ne onde mécanique progressive est donc une vibration de la matière sans son transport, d’où la
propagation d’énergie. Comme toute onde, l’onde longitudinale qui nous intéresse ici possède une vitesse
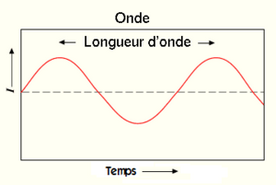
de propagation (célérité), une longueur d’onde nommée λ correspondant à la période spatiale. Elle possède
aussi une période temporelle puisque les ondes sont périodiques.
Aussi, les ondes longitudinales sont modélisées par des courbes sinusoïdales montrant bien les extremums
d’intensité formant des crêtes et des creux : c’est l’amplitude de l’onde. (figure 4)

Fig.4
A
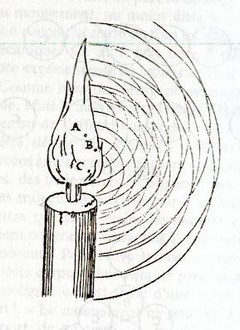
insi dans son traité de la lumière, Huygens a représenté les ondes lumineuses partant de tous les points
de la bougie ci-dessous (figure 5). Elles sont représentées par les arcs de cercle ici. Les fronts d’ondes, c'est-à-dire
les surfaces qui représentent l’avancement des ondes sont des sphères, les ondes se propagent donc dans
toutes les directions de façon sphériques.

Fig.5
P
our Huygens, tout l’univers est rempli de ces particules qu’il nomme éther. Effectivement, l’oscillation
de ces particules formerait selon Huygens des ondes qui se propagent dans toutes les directions de façon
circulaire suivant un front d’onde. Pour rendre sa thèse plausible, Huygens, se base sur le fait que la
théorie corpusculaire n’explique pas le fait que lorsque deux faisceaux lumineux se croisent, ils ne varient
pas. Pourtant, d’après la théorie corpusculaire, l’inertie des particules croisant une infinité d’autres
trajectoires devrait avoir un impacte visuel. Huygens fait donc appel au pendule de Newton, dont les boules
métalliques en suspension font office de particules d’éther.
V
oici, l’écrit de Huygens : “ quand on considère l’extrême vitesse dont la lumière s’étend de toutes parts,
et que quand il en vient de différents endroits, même de tout opposés, elle se traversent l’une l’autre sans
s’empêcher, on comprend bien que quand nous voyons un objet lumineux, ce ne saurait être par le transport
d’une matière, qui depuis cet objet s’envient jusqu’à nous, ainsi qu’une balle ou une flèche traverse l’air
: car assurément cela répugne trop à ces deux qualités de la lumière, et surtout à la dernière. C’est donc
d’une autre manière qu’elle s’étend, et ce qui peut nous conduire à la comprendre c’est la connaissance que
nous avons de l’extension du son dans l’air. ” Traité de la lumière.

Fig.6
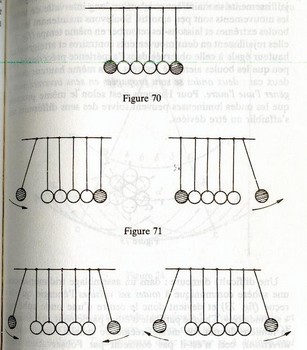
L
orsque l’on soulève et que l’on lâche une première boule (à gauche), la boule à l’extrémité se soulève
(à droite), il y a eu propagation d’une onde longitudinale et le mouvement s’est transmi ainsi que l’énergie
(cinétique en l’occurrence). Maintenant, lorsque l’on soulève les deux boules aux extrêmes et que l’on les
lâche, elles jaillissent en deux mouvements contraires et atteignent une hauteur égale à celle observée
dans la précédente expérience (figure 6). Ainsi, la conclusion et faite, pour Huygens, c’est selon ce même processus
que les ondes lumineuses peuvent se croiser sans s’affaiblir ou être déviées. L’existence de l’éther est
admise.
C’
est donc une toute nouvelle vision de la lumière que Huygens propose. Une vision ondulatoire à l'image de
"l’extension du son dans l’air". Huygens, élève de Descartes fait tanguer l’édifice de Newton. L’arrivée
de l’éther, permet ainsi d’interpréter mieux que toute autre théorie l’optique géométrique de Descartes et
ouvre la voie à des expériences que nous nommerons cruciales. Nous assistons au cours de l’histoire à une
véritable révolution en physique.
P
our Newton, la réflexion et la réfraction découlent tout simplement de l’intensité de la force qu’exerce
le milieu sur les particules de lumière constituant le rayon lumineux. Or comme nous l’avons vu, Huygens
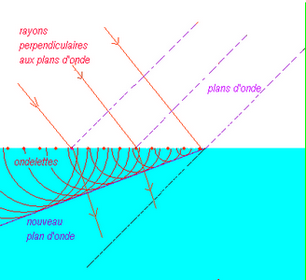
pense que la lumière est formée d’ondes sphériques qui sont assimilées à une onde plane (AC). Une onde plane
est une onde dont les fronts d’onde apparaissent comme des plans infinis tous perpendiculaires à une même
direction. (figure 8)
L
a grande nouveauté dans la théorie de Huygens est que non seulement il peut tout autant que la théorie de
Newton interpréter la réflexion et la réfraction mais aussi expliquer le devenir de la lumière.
E
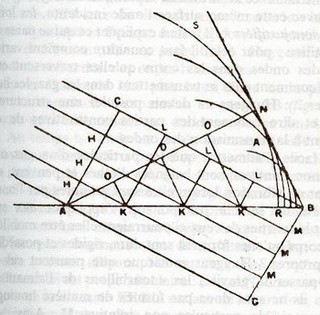
n ce qui concerne la réflexion de la lumière, le principe ne change pas vraiment, d’après le schéma
ci-dessous, extrait du traité de la lumière de Huygens, l’onde plane se propage selon des rayons lumineux
qui lui sont perpendiculaires avec une vitesse v représenté par HM.(figure 8)

fig.7

fig.8
H
uygens considère AB la séparation des deux milieux. Lorsque l’onde arrive en B, l’ondelette émise
du point A dans le premier milieu atteind les points de la demi-sphère, SNR, de même pour les points K,
les ondelettes émises arrivent en des points situés sur des demi-sphères de rayon de plus en plus petit
puisque ces points K ont été touchés plus tard par l’onde incidente. Comme nous l’avons vu, toutes ces
ondelettes ont la même enveloppe commune, NB étant le plan d’onde, c’est aussi l’onde plane réfléchie.
Et donc, comme elle fait un angle égal à celui que fait avec la même surface l’onde incidente, les
lois de la réflexion sont bien justifiées.
E
n ce qui concerne la réfraction, contrairement à la théorie corpusculaire qui stipulait qu’au passage
d’un changement de milieu, la vitesse de la lumière augmente, la théorie ondulatoire affirme tout le
contraire. En effet, Huygens affirme que l’éther se trouve partout. Ainsi dans un milieu plus dense,
l’éther se trouve gêné par les parties constitutives du solide. Les vibrations sont donc gênés et l’onde
ralenti. Donc quelque soit la manière dont l’onde est transmise, la vitesse de la lumière doit
être plus faible dans un solide, ou liquide que dans l’air.
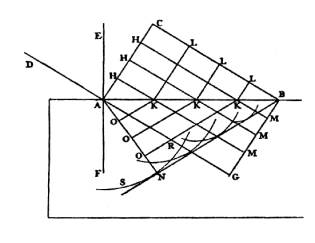
R
eprenons l’exemple d’une onde AC arrivant sur une surface de séparation Air/Verre AB (figure 9). On s’intéresse
ici aux ondes dans le second milieu. Lorsque tous les points K de la surface frappent successivement,
ils deviennent le centre d’onde demi-sphérique qui se propage dans le second milieu avec une vitesse
v plus faible et avec comme enveloppe commune le plan d’onde NB. NB apparaît comme l’onde réfractée.
Et le rayon réfracté représentatif AN se rapproche de la normale EF. Ainsi, Huygens rend compte de
la réfraction de la lumière.

Fig.9

Fig.10
I
l en vient donc à montrer que la justification des lois de Descartes ne peuvent se faire
seulement si les vitesses de propagation des ondes sont inversement proportionnelles aux indices des
milieux traversés. Ce que Fermat, grand mathématicien français avait établi dans son théorème,
le théorème de Fermat qui affirme que : "La lumière se propage d'un point à un autre sur une trajectoire
telle que la durée du parcours soit minimale". Huygens change ainsi dans la formule dans la loi de Descartes :
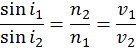
E
n conclusion, la notion de rayon lumineux est liée à la notion de front d’onde, ou plan d’onde plane.
Ainsi, il manque seulement une expérience que l’on qualifie de cruciale pour ainsi montrer que la
vitesse de la lumière est plus faible dans un milieu plus dense allant contre de la théorie de Newton.